第零章 绪论
基本概念
数据(Data):对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素(Data Element):数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
数据项(Data Item):是数据的不可分割的最小单位。
数据对象(Data Object):是性质相同的数据元素的集合,是数据的一个子集。
数据结构(Data Structure):是相互之间存在一种或多种特定关系的数据元素的集合。数据元素相互之间的关系称为结构(structure),数据结构是带“结构”的数据元素的集合。
数据结构包括逻辑结构和存储结构两个层次。
逻辑结构:描述的是数据元素之间的逻辑关系。根据数据元素之间关系的不同特性,通常有下列四类基本结构:集合、线性结构、树结构、图结构。
存储结构:数据结构在计算机中的存储称为数据的存储结构,也称为物理结构。两种基本的存储结构:顺序存储结构和链式存储结构。
顺序存储结构:所有元素依次存放在一片连续的存储空间中。通常,元素在存储器中的相对位置可以表示数据元素之间的逻辑关系。
链式存储结构:为了表示结点之间的关系,需要给每个结点附加指针字段,指向相关的其他结点。
数据类型(Data Type):一个值的集合和定义在这个值集上的一组操作的总称。
抽象数据类型(Abstract Data Type,ADT):
一般指由用户定义的、表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
具体包括三个部分:
- 数据对象
- 数据对象上的关系的集合
- 数据对象的基本操作的集合
对于数据结构的表示方法及操作的实现,与存储结构有关。
算法分析部分见笔记--大二--算法分析与设计--《算法》笔记--函数的增长章节。
概念详解
上面的概念看看就好了。我挑一个重点的概念讲讲,就是这个抽象数据类型。
我建议把它当作一个类来看,C++和Java应该都学过类。一个抽象数据类型要包含数据对象,也就是类里面的成员。关系集合和操作集合可以看作类的函数。
ADT是比较重要的概念,每个数据结构都会对应一个ADT,这个东西可能会根据不同的实际问题进行微调,但大体的思路不会变。
第一章 线性表
基本概念
线性表:具有相同类型的n个数据元素的有限序列。
顺序表:用连续的一整块内存存储数据的线性表。
链表:用分散的一块块等大小的内存存储数据的线性表,每块内存用next指针链接成一条链。
线性表的基本运算:增删查改,打印等。
顺序表的抽象数据类型
这里给出C++书写的定义。
#define MAXN 100
class ArrayList{
public:
int array[MAXN];
private:
void insert(int, int);
void del(int);
int find(int);//return pos
void modify(int, int);
void myPrint();
//...
}链表的抽象数据类型
这里给出C++书写的定义。
typedef struct LinkedList{
int data;
struct LinkedList* next;
}Node;
Node* insert(Node*, int, int);
Node* del(Node*, int);
int find(Node*, int);
Node* modify(Node*, int, int);
void myPrint(Node*);
//...解析
抽象数据类型最好按照上述模板定义。在定义的时候,一定要确保几个最基础的函数运算的定义是完备的,即不会出现各种运行时错误&未定义行为。在确保基础运算是正确且完备的基础上,再去实现别的功能。
附加一份可用的链表模板代码。
#include <bits/stdc++.h>
using namespace std;
typedef struct LinkedNode{
int elem;
struct LinkedNode* next;
}node;
void createLinkedList(node* head){
head->elem = 0;
head->next = NULL;
}
node* newNode(int elem){
node* p = (node*)malloc(sizeof(node));
p->elem = elem;
p->next = NULL;
return p;
}
void addNode(node* head, int elem){
node* p = head;
while(p->next)
p = p->next;
node* newNode = (node*)malloc(sizeof(node));
newNode->elem = elem;
newNode->next = NULL;
p->next = newNode;
}
void addNode(node* head, int n, int elem){
node* p = head;
for(int i = 0; i < n-1; i++){
if(!(p->next)){
printf("Index Out of Bound Error.\n");
return;
}
p = p->next;
}
node* addedNode = newNode(elem);
node* tmp = p->next;
p->next = addedNode;
if(tmp)
addedNode->next = tmp;
}
void deleteNode(node* head, int n){
node* p = head;
for(int i = 0; i < n-1; i++){
if(!(p->next)){
printf("Index Out of Bound Error.\n");
return;
}
p = p->next;
}
node* tmp = p->next;
if(!tmp){
printf("Index Out of Bound Error.\n");
return;
}
p->next = tmp->next;
free(tmp);
}
int search(node* head, int n){
node* p = head;
for(int i = 0; i < n; i++){
if(!p){
printf("Index Out of Bound Error.\n");
return -1;
}
p = p->next;
}
return p->elem;
}
void modify(node* head, int n, int elem){
node* p = head;
for(int i = 0; i < n; i++){
if(!p){
printf("Index Out of Bound Error.\n");
return;
}
p = p->next;
}
p->elem = elem;
}
void deleteList(node* head){
int n = 0;
node* p = head;
while(p){
p = p->next;
n++;
}
for(int i = n-1; i > 0; i--)
deleteNode(head, i);
}
void myPrint(node* head){
if(!(head->next))
return;
node* p = head->next;
while(p){
printf("%d ", p->elem);
p = p->next;
}
printf("\n");
}
int main(){
node* head = (node*)malloc(sizeof(node));
createLinkedList(head);
while(1){
printf("Enter a number to choose an operation:\n1. add a Node to the rear of this LinkedList\n");
printf("2. add a Node to any pos of this LinkedList\n");
printf("3. delete a Node from this LinkedList\n");
printf("4. search an element in the list\n");
printf("5. modify a node\n");
printf("6. print the list\n");
printf("7. delete the list\n");
printf("8. exit the program\nCommand:");
int cmd;
scanf("%d", &cmd);
if(cmd == 1){
printf("Enter an element:");
int elem;
scanf("%d", &elem);
addNode(head, elem);
}
if(cmd == 2){
int elem, pos;
printf("Enter an element:");
scanf("%d", &elem);
printf("Enter a pos:");
scanf("%d", &pos);
addNode(head, pos, elem);
}
if(cmd == 3){
int pos;
printf("Enter a pos:");
scanf("%d", &pos);
deleteNode(head, pos);
}
if(cmd == 4){
int pos;
printf("Enter a pos:");
scanf("%d", &pos);
printf("%d\n", search(head, pos));
}
if(cmd == 5){
int elem, pos;
printf("Enter an element:");
scanf("%d", &elem);
printf("Enter a pos:");
scanf("%d", &pos);
modify(head, pos, elem);
}
if(cmd == 6){
myPrint(head);
}
if(cmd == 7){
deleteList(head);
free(head);
return 0;
}
if(cmd == 8){
return 0;
}
}
return 0;
}栈与队列
栈:只允许对一端进行操作的线性表。
队列:只允许两端分别进行入和出的线性表。
栈和队列都是操作受限的线性表。它们的限制是人为强加上去的,但是受限制的操作可以带来超出数组、链表的功能。
栈的抽象数据类型
这里给出顺序存储的C++定义。
class Stack{
private:
int a[MAXN];
int top;
int bottom;
public:
int pop();//return and remove the top elem
void push(int);
int peek();//return the top elem
bool isEmpty();//return true if the stack is empty
//...
}一般来说,栈的成员变量包含:
- 数组,用于存储数据
- top指针,用于入栈和出栈的操作
- bottom指针,用于判断栈是否下溢
栈的基本函数包括:
- 出栈,返回并移除栈顶元素
- 入栈,将元素压入栈顶
- 其他辅助函数...
队列的抽象数据类型
这里给出顺序存储的C++定义。
class Queue{
private:
int a[MAXN];
int front;
int rear;
public:
int dequeue();//return and remove the top elem
void enqueue(int);
//...
}一般来说,队列的成员变量包含:
- 数组,用于存储元素
- 队首指针front,用于出队列操作
- 队尾指针rear,用于入队列操作
队列的函数包括:
- 出队列,返回并移除队首元素
- 入队列,将元素压入队尾
- 其他辅助函数...
定义详解
关于栈的定义,讲顺序和链式两种方法。
首先是顺序定义。
一般来说,bottom指针的不需要动的,固定大小为0。至于为什么要有这个bottom,在链式定义中它是很有用的。为了定义统一,在顺序定义中也加入这个变量。
top指针一般初始值为0,也就是top==bottom==0的时候,表示栈是空的。在这个时候,不能进行出栈操作。否则会产生栈下溢(StackUnderflow Error)。
如果top>=MAXN,则不能进行入栈操作。否则会产生栈上溢(StackOverflow Error)。
在执行入栈出栈的时候,注意不需要真正地去删除某个元素。只需要移动指针,只考虑top~bottom中间的范围即可,其他的作为备用存储空间,里面存储的元素值不需要考虑。
然后是链式定义。
顺序定义的栈是基于顺序表的,那么链式定义的栈就是基于链表的。
这里的链表需要初始化一个head结点,指向NULL。后续的结点链在head后面。每个结点需要一个pre指针和一个next指针,形成双向链表,方便出栈操作。
与顺序表不同的是,需要一个bottom指针指向链表首结点,即head结点。
top指针也初始化为head结点。之后的入栈操作,相当于在top后面添加一个结点。因为top始终指向链表尾部,所以所有的入栈都是在链表尾部增加结点。
在进行出栈操作的时候,则是删除链表尾部的结点,这里的删除不是移动指针了,而是释放这个结点的内存并且将top指针向前移动一格。
链式定义的栈拥有动态的内存空间,不会造成内存的浪费。但是在出入栈时的操作,比顺序表的操作更加复杂,但不会造成渐进时间复杂度的增级。
队列的顺序、链式定义可以类比于栈。顺序入队出队的操作只需要移动指针即可,链式的入队出队操作则需要头插、尾删函数的支持,在这里就不详细讲了,可以根据上述链表的定义、栈的定义自己实现一下。
重点是顺序存储的队列。由于入队是rear指针增1,出队是front指针增1。在反复出队入队后,会出现rear==MAXN && front != 0的情况,即数组并没有用满,但是rear后面没有内存空间,无法入队了。这种情况称为队列的假满。
这一问题可以通过环形队列的方法解决。环形队列即将下标为0的元素与下标为MAXN-1的元素相连,将一整块内存抽象为一个环形。这样rear就可以突破MAXN的限制,进入0,开始利用之前出队空出来的内存。
然后问题又来了。在上述环形队列中,队满的情况,有front==rear,队空的情况,也有front==rear。因此需要一个标签来判断是队空还是队满(也可以记录元素的数量,判断是否等于MAXN)。
还有一种方式,额外申请一块内存,也就是令数组大小为MAXN+1。每次进队后,先令rear=(rear+1)%MAXN,判断rear是否赶上了front,如果赶上则报告队满。但实际上,队列还有一块内存可用,只是为了解决上述问题,需要将这块内存始终置空。
其他存贮方式
压缩存贮
定义结构体如下:
typedef struct node{
int i;//代表原数组中元素k的下标
int k;//代表原数组中的元素
}Node;对于一个线性表,例如\{1,0,0,0,2,0,0,3\},申请一个新的结构体数组Node^*\space n,n[0]={0,1}......
这样的压缩方式适用于线性表中重复且不必要的元素较多的情况,可以将无用元素剔除,只保留有意义的元素。
索引存贮
定义结构体如下:
typedef struct node{
int key;
enum data;
}Node;对于线性表Node^* n,建立m个子表Node^* Fm,将原线性表划分到这些子表中。假设x_1,x_2,...,x_m分别为指向F_1,F_2,...,F_m首结点的指针,则X=(x_1,x_2,...,x_m)就构成索引线性表。
“顺序-索引-链接”存贮方法:子表采用链接存储,便于插入和删除。索引表采用顺序存储,便于查找。在索引表X的结点中增加了一个界限字段。对于子线性表E中的任一结点的键值都小于x中的界限值。这样查找一个key值时,只需要搜索大于它的最小x值指向的子链表即可。

索引表可以套娃存储,即对索引表建立索引表。
散列存贮(哈希表)
对于键值key,用一个哈希函数h(x)使得每个key对应唯一一个哈希值。key对应的结点存放在数组T中的位置就由这个哈希值决定。这个数组T就称为哈希表。
一般来说,很难找到一个函数h,使得每个键值都有唯一的哈希值与之对应。因此一般使用不一一对应的简单哈希函数h(x)=key mod n,n为哈希表大小。这样一来,有可能会出现哈希值冲突的情况,即key值不同,h(key)相同的情况。
解决冲突一般有两种方法:
- 开放寻址法。存储时,将有冲突的后续哈希值顺次+1,直到与任何元素都不冲突。查找时,先查找原哈希值的位置,如果不一样,则进行顺序查找,直到找到目标为止。
- 拉链法。存储时,采用“顺序-索引-链接”存贮方法,让每个哈希值指向一个子链表,如果产生哈希值的冲突,则在这个哈希值指向的子链表末尾插入冲突的元素即可。查找时,先查找原哈希值的为止,然后搜索哈希值指向的子链表,直到找到目标为止。

广义表
各种表、元素的嵌套。
递归表:考虑表A:(1,(2,3),A),将自己作为自己的元素,称为递归表。
广义表的递归算法
暂略,待补充。
习题
暂略,待补充。
第二章 串
基础概念
串:假设V是程序设计语言所使用的字符集,由字符集V上的字符所组成的任何有限序列,称为字符串,简称为串。
串长:串包含的字符个数。
空串:不包含字符的串。
模式匹配算法
假设T和P是两个给定的串,在T中寻找等于P的子串的过程称为模式匹配。T代表正文(Text),P代表模式(Pattern)。通常来说,T的长度远大于P的长度。
输入串T和串P,返回一个布尔值,如果T中包含等于P的子串,则返回值为true;反之则返回值为false。
简单算法
详细定义看书就行。这里讲直观的步骤。
将串P与T首位对齐,逐字符比较,如果比较结束完全匹配,则返回true;如果比较出现了不匹配的情况,则将P整体向后移动一位,再重复上述过程。
习题
待补充
第三章 内部排序
插入排序
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
i = j-1
while i > 0 and A[i] > key
A[i+1] = A[i]
i = i-1
A[i+1] = key循环不变式的三条性质
初始化:循环的第一次迭代之前,它为真。
保持:每次循环迭代完成之后,在下次迭代开始之前它依旧保持为真。
终止:在循环终止后,该不变式为我们提供一个有用的性质,能够帮助证明算法的正确性。
插入排序的循环不变式为:对于给定的小于n的正整数p,保证A=[A_1,...,A_p]是一个有序表。
以上表述可以描述为:维护一个从A_1到A_p的有序表。
说明INSERTION-SORT在数组A=〈31,41,59,26,41,58)上的执行过程。
解:
初始化p=1,每次循环p=p+1.
31,41,59,26,41,58 p=2,p=3
26,31,41,59,41,58 p=4
26,31,41,41,59,58 p=5
26,31,41,41,58,59 p=6,终止。
可以根据上述循环不变式的描述来验证题解。
选择排序
2.2-2
考虑排序存储在数组A中的n个数:首先找出A中的最小元素并将其与A[1]中的元素进行交换。接着,找出A中的次最小元素并将其与A[2]中的元素进行交换。对A中前n一1个元素按该方式继续。该算法称为选择算法,写出其伪代码。该算法维持的循环不变式是什么?为什么它只需要对前n-1个元素,而不是对所有n个元素运行?用记号给出选择排序的最好情况与最坏情况运行时间。
解:
SELECTION-SORT(A):
for i = 1 to n-1
for j = i+1 to n
if A[j]<A[i]
exchange A[i] with A[j]循环不变式:
在第i次循环时,A[1]是第1小的数,A[2]是第2小的数...A[i-1]是第i-1小的数。
证明:
初始化:在进入循环之前,A[1..i-1]有序,且保证A[1]是第1小的数,A[2]是第2小的数...A[i-1]是第i-1小的数。
保持:内层循环从A[i+1]开始,逐个与A[i]比较,如果比A[i]小,则与A[i]交换位置。因此内层循环结束后,能保证A[i]是A[i...n]中最小的数。
又因为任取j \in {1,...,i-1},有A[j] \leqslant A[i],所以A[i]是A中第i小的数。循环不变式保持。
终止:当 i>n-1 时,循环终止。此时A[1..n-1]有序,且保证A[1]是第1小的数,A[2]是第2小的数...A[n-1]是第n-1小的数。
由上述结论,任取j \in {1,...,n-1},有A[j] \leqslant A[n],所以A[n]是A中第n小的数。
综合上述三条性质,得出:在表A中,设n=A.length,A[i](i \in {1,2,...,n})总是A中第i小的数。也就是表A中元素升序排列。
据数学归纳法证明得知,此算法的外层第i次循环保证了A[i]元素是所有元素中第i小的;循环至n-1次时,A[1]是第1小的数,A[2]是第2小的数...A[n-1]是第n-1小的数;假设A[n]需要移动,那么A[n]就不是A中第n小的数,与上述结论矛盾;所以无需对A[n]进行比较。
最好情况:O(n);最坏情况:O(n^2)。
归并排序
MERGE(A, p, q, r)
n1 = q-p+1
n2 = r-q
let L[1..n1+1], R[1..n2+1] be new arrays
for i = 1 to n1
L[i] = A[p+i-1]
for j = 1 to n2
R[j] = A[q+j]
L[n1+1] = INF
R[n2+1] = INF
i = 1
j = 1
for k = p to r
if L[i] <= R[j]
A[k] = L[i]
i = i + 1
else A[k] = R[j]
j = j + 1
MERGE-SORT(A, p, r)
if p < r
q = (p+r)/2
MERGE-SORT(A, p, q)
MERGE-SORT(A, q+1, r)
MERGE(A, p, q, r)递归树
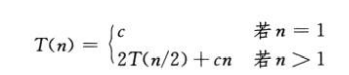
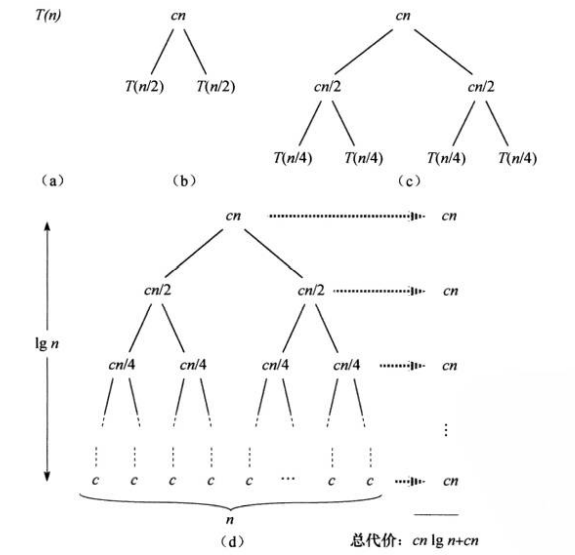
快速排序
伪代码和维护的性质
QUICKSORT(A, p, r)
if p < r
q = PARTITION(A, p, r)
QUICKSORT(A, p, q-1)
QUICKSORT(A, q+1, r)PARTITION(A, p, r)
x = A[r]
i = p-1
for j = p to r-1
if A[j] <= x
i = i+1
exchange A[i] with A[j]
exchange A[i+1] with A[r]
return i+1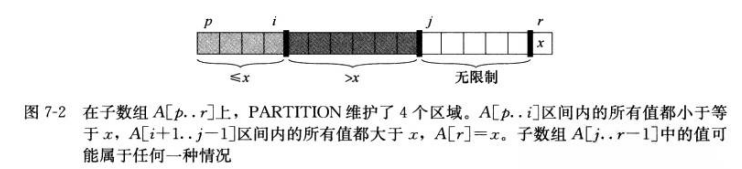
性能分析
最坏情况性能分析
最坏情况发生在每次划分的子问题包含n-1个元素和个元素的时候。
可以写出递归式:T(n)=T(n-1)+T(0)+\Theta (n)=T(n-1)+\Theta (n)。
求解递归式得到时间复杂度为\Theta (n^2)。
平衡情况的性能分析
假设划分为9:1,得到递归式:T(n)=T(9n/10)+T(n/10)+cn,求解递归式得到时间复杂度为O(nlgn)。
随机化
RANDOMRIZED-PARTITION(A, p, r)
i = RANDOM(p, r)
exchange A[r] with A[i]
return PARTITION(A, p, r)RANDOMRIZED-QUICKSORT(A, p, r)
if p < r
q = RANDOMRIZED-PARTITION(A, p, r)
RANDOMRIZED-QUICKSORT(A, p, q-1)
RANDOMRIZED-QUICKSORT(A, q+1, r)基数排序
根据数字位数排序,从低位到高位,每次使用稳定的排序算法。
引理8.3:给定n个d位数,其中每一个数位有k个可能的取值。如果RADIX-SORT使用的稳定排序方法耗时\Theta (n+k),那么它就可以在\Theta (d(n+k))时间内将这些数排好序。
桶排序
将数组元素所在的区间划为几个桶,将数字装桶后,对每个桶使用插入排序(或者其他稳定的排序算法),期望时间复杂度为\Theta (n)。